Now, if I were to take two numbers next to each other on the pattern and divide them by each other, I would get an answer approximate to phi. The further the two number are on the pattern, the closer they are to it. For example: 21÷13≈1.6153 while 144÷89≈1.6179 (phi≈1.61803).
A very bizarre way that the Fibonacci Sequence can be shown is in honeybees. Each female honeybee has a mother and a father (you might say, "duh"), but male honeybees strangely only have a mother ("what?") since males are produced from an unfertilized egg. Below is a family tree of a male bee: (The circle with the arrow means male while the plus means female.)

So to start out with, the bee here has one parent, a mother.
He has two grandparents.
He has three great grandparents.
He has five great great grandparents.
Is this pattern starting to look familiar? Yes, it is the Fibonacci Sequence.
The sneezewort (Achillea ptarmica) is a plant that also demonstrates the Fibonacci numbers in its branch numbers and leaves.

On a lot of flowing plants (not all), the flowers' petals tend to be a Fibonacci number (or the average of the number of petals is a Fibonacci number). In my yard, I had a hibiscus and an african violet both with five petals. Clovers would be a Fibonacci flower even though they can have four leaves because the average amount of clovers have three leaves. Other Fibonacci flowers include buttercup (5 petals), delphiniums (8 petals), ragwort (13 petals), black-eyed susan (21 petals), and plantain (34 petals).
— Alec
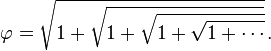 and stumble upon the fact that no matter what number you put for "x", you end up with the same number? (Ok, I seriously doubt you have, but if you did that, you would always end up with a number called phi.)
and stumble upon the fact that no matter what number you put for "x", you end up with the same number? (Ok, I seriously doubt you have, but if you did that, you would always end up with a number called phi.)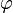


 and
and 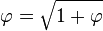
 .
.




 ^^^^^^^^^^^^^^^^^^^^^^^^^^^
^^^^^^^^^^^^^^^^^^^^^^^^^^^




 This continuous curvature can be found in many natural things like pine cones, sunflowers, chambered nautilus etc.
This continuous curvature can be found in many natural things like pine cones, sunflowers, chambered nautilus etc.